Introdução

Dada a rapidez com que a epidemia/pandemia estava progredindo, as estimativas contam com heurísticas relativamente simples, em vez de análises abrangentes, que levam mais tempo para serem discutidas e testadas. A ênfase está na velocidade e nos dados continuamente atualizados, em vez de análises sofisticadas.

As análises mais sofisticadas estão sendo feitas em paralelo, sendo elas:

Aplicação e desenvolvimento de um modelo matemático epidemiologico levando em conta: a fração de indivíduos que se tornam graves, tempo de isolamento social, grau de mobilidade, probabilidade de contágio variada, entre outros aspectos;
Desenvolvimento de um modelo matemático de simulação espacial do contágio, levando em consideração aspectos geograficos como tamanho de uma cidade, densidade populacional, entre outros aspectos..

Background do modelo simples - crescimento populacional baseado na Lei de Malthus:

O modelo exponencial de crescimento populacional proposto por Malthus pode ser aplicado ao contexto inicial do presente caso, o da dissiminação da doença.

O modelo baseado na Lei de Malthus descreve o aumento populacional da seguinte forma:

a taxa de mudança da população de sociedades humanas, espécies de animais, insetos ou colônias de bactérias é proporcional (\(\propto\)) ao tamanho da população, sendo \(N(t)\) a população no instante de tempo \(t\), onde podemos assumir que a população no instante de tempo inicial \(t=0\) é alguma valor, chamado de \(N_0\). Assim o modelo que descreve essa taxa de mudança é dado pela equação diferencial:

\[ \frac{dN(t)}{dt} \propto N(t) \]

A proporcionalidade (\(\propto\)) pode ser transformada em uma igualdade (\(=\)) com a multiplicação de uma constante qualquer, chamada aqui de \(r\), assim temos:

\[ \frac{dN(t)}{dt} = rN(t) \] onde \(r\) para esse caso é a taxa líquida da população, definida como a diferença entre as taxas de nascimento e óbito. O valor dessa constante \(r\), por exemplo, se for um valor de \(0.015/dia\) pode representar uma taxa de crescimento de 15 pessoas, por dia, para cada grupo de 1000 pessoas.

A equação (classificada como uma equação linear de primeira ordem com coeficientes constantes), dada uma condição inicial, de que no instante inicial, aqui denominado tempo zero \(t=0\), é especificada como uma quantidade, \(N(t=0) = N_0\), sendo, \(N_0\) uma quantidade inicial de pessoas, possui a seguinte solução.

\[ N(t) = N_0e^{rt} \]

Assim, a suposição de que a população aumenta a uma taxa proporcional ao tamanho dessa população implica que a população aumenta exponencialmente com o tempo. Esse modelo de mudança populacional é conhecido como crescimento exponencial ou lei de Malthus. Esse modelo publicado pelo economista britâncio Thomas Malthus (1766-1834), embora seja extremamente simples ele é bem aplicado pelo menos para períodos limitados de tempo, geralmente períodos iniciais. Para longos períodos de tempo outros modelos de crescimento populacional como por exemplo o modelo de crescimento logístico pode ser aplicado.

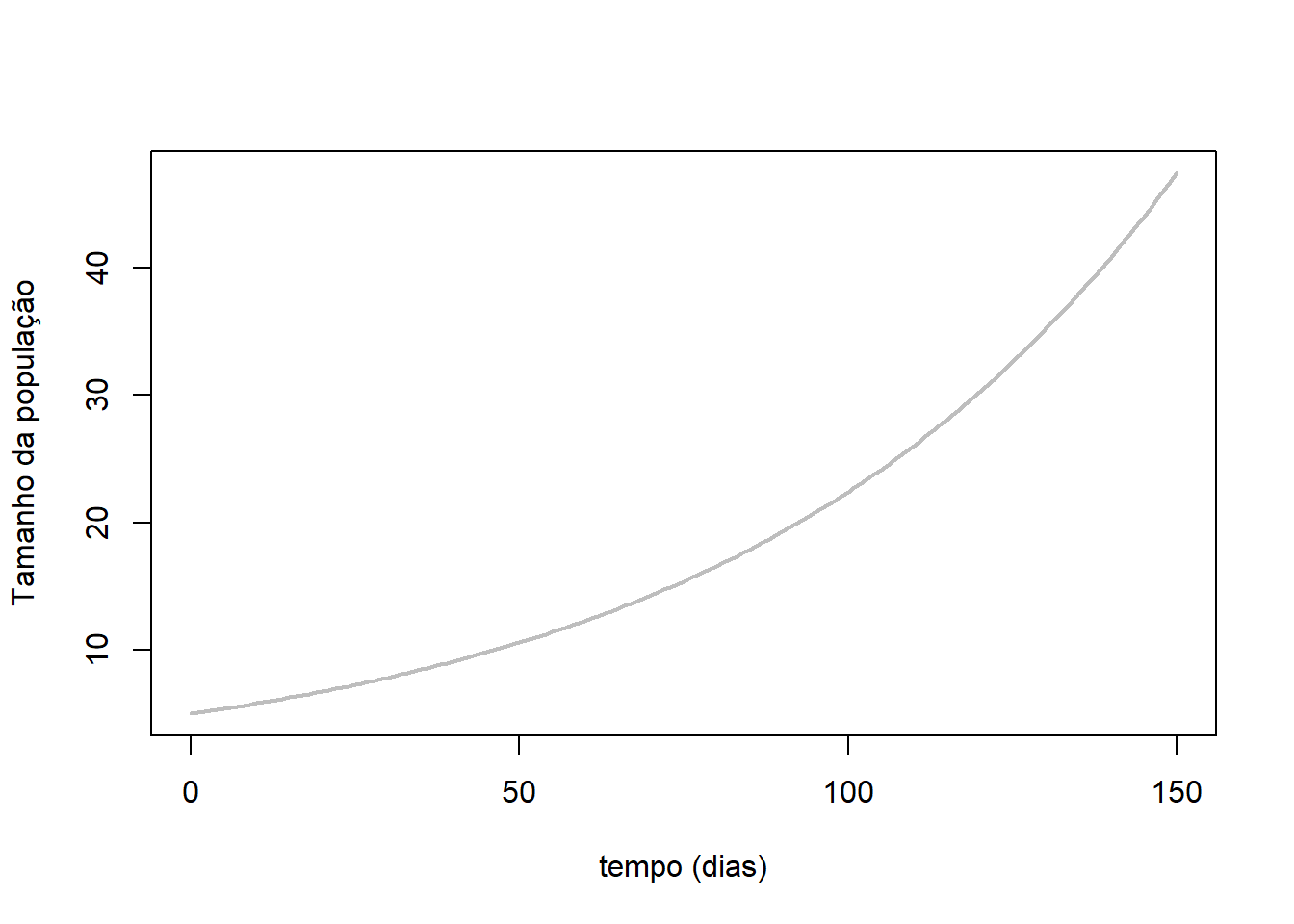
Exemplo de modelo exponencial de crescimento

Métodos

Números bruto de casos confirmados

Nossos dados vêm do Brasil.IO, que é atualizado diariamente. Esses dados relatam o número acumulado de indivíduos confirmados com infecção de covid-19 (\(I(t)\)) e o número de óbitos (\(D(t)\)) em cada cidade do país.

Modelo de crescimento e previsão de casos confirmados de covid-19 [deprecated - substituido pelo modelo de Gompertz]

Estamos interessados em saber como o número de casos confirmados vai mudar no curto prazo, e para isso utilizaremos o modelo exponencial. Assim, assumimos que casos confirmados seguem um modelo de crescimento exponencial em fases inciais da pandemia, tal que \(E[I(t)] = I_0e^{rt}\), que é o que se espera (valor esperado) em média do número de casos confirmados, ou seja o modelo exponencial \(I(t) = I_0e^{rt}\), onde o valor dado pelo modelo será considerado um valor médio.

Sabe-se que a dinâmica do crescimento do número de infectados é mais complexa do que isso, e para tanto vários modelos epidemiológicos compartimentais como SIR, SEIR entre outros podem ser utilizados, bem como modelos probabilísticos.

Os dados disponibilizados até o presente momento estão relacionados com a fase inicial da dissiminação da doença e esse tópico trata somente de uma análise de curto prazo e para isso o modelo exponencial pode fornecer uma aproximação razoável.

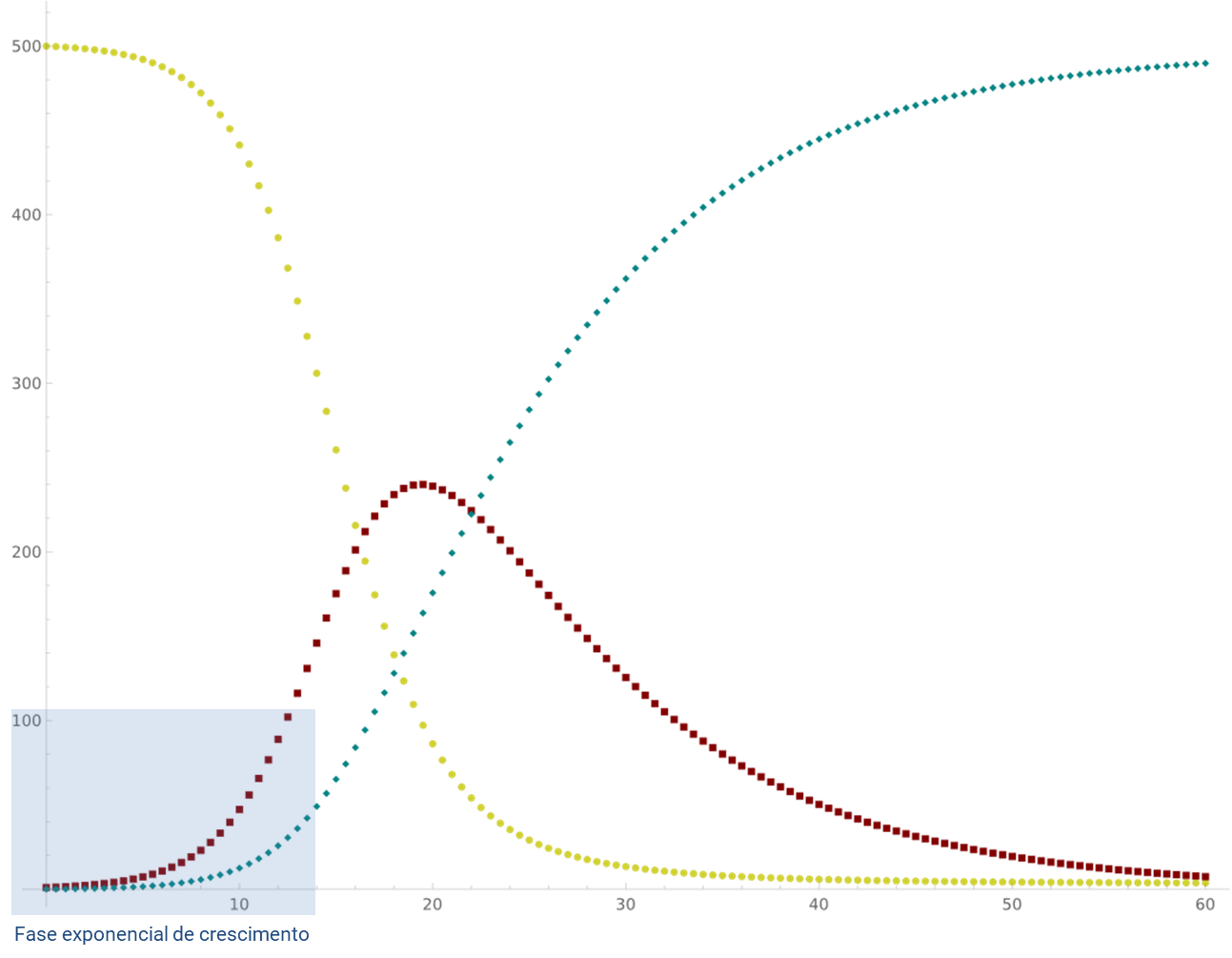
Exemplo de modelo epidemiológico compartimental

Para ajustar esse modelo exponencial aos dados obtidos, realizamos o processo de linearização do modelo, aplicando logaritmo natural de ambos os lados da equação, produzindo \(ln(I(t)) = rt + ln(I_0)\), dessa forma podemos ajustar por regressão linear simples as variáveis \(ln(I(t))\) e \(t\). A inclinação desse ajuste é uma estimativa da taxa de crescimento intrínseca, \(r\).

Várias estratégias de ajuste desse modelo aos dados pode ser efetuada, por exemplo com base nos últimos (5,10,15,20,…) dias de dados de \(I(t)\), com isso realizamos a extrapolação, ou seja predição do modelo ajustado para entender com base em dados observados o que ocorrerá daqui a 7 dias ou mais no futuro, de acordo com o modelo exponencial ajustado.

O ajuste e a extrapolação/predição foram efetuados com o modelo transformado (linearizado) em termos \(log\) natural (com intervalos de predição de 95%) e esse \(log\) dos números de casos confirmados esperados é transformado novamente na escala original para produzir os dados que são apresentados nos gráficos.

As intervenções de saúde pública estão mudando rapidamente a taxa de crescimento, isso pode ser visto como desvios da linha reta esperada no gráfico quando apresentado em escala \(log\).

Nessas situações, quando a taxa de crescimento estiver caindo rapidamente (é onde supostamente a “curva está se achatando”), neste caso as previsões desse modelo exponencial serão enviesadas para cima.

Os gráficos serão apresentados em escala linear e escala \(log\).

Tempo de duplicação

O tempo de duplicação (\(t_d\)) é uma medida intuitiva da rapidez com que a doença está crescendo. Ele relata o número de dias para os confirmados dobrar de tamanho e é calculada da seguinte forma, considerando o quantidade confirmados atual dividido quantidade de confirmados no instante inicial sendo igual a 2, ou seja

\[ \begin{aligned} \frac{I(t)}{I_0} &= 2\\ \\ \frac{I_0e^{r\color{red}{t_d}}}{I_0} &= 2\\ \color{red}{t_d} &= \frac{ln(2)}{r}\\ \end{aligned} \] Dessa forma o tempo de duplicação pode ser calculado diretamente a partir das estimativas de \(r\).

Taxa de crescimento

As intervenções de saúde pública visam reduzir a transmissão de vírus e, assim, reduzir o crescimento do número de casos ativos. As primeiras indicações de sucesso da intervenção se manifestarão em taxas de crescimento mais baixas (provavelmente irá refletir após dez dias da intervenção, no caso da covid-19).

A taxa de crescimento per capita pode ser calculada todos os dias como

\[ G(t) = \frac{I(t)-I(t-1)}{I(t-1)} \]